峳壆恀擇挊丂乽恖岺抦擻奣榑丂乮戞俀斉乯乿丂嫟棫弌斉丂2004.10.1
丂丂丂丂丂丂丂丂丂丂亙Top儁乕僕亜丂亙峳壆尋媶幒傊亜
墘廗栤戣偺夝摎椺乮戞侾乣俆復乯丂丂丂丂嵟廔峏怴丗2004.10.1
戞侾復
墘廗栤戣側偟
戞俀復
2.1丂悈嵎偟栤戣偺忬懺嬻娫偼恾2.3 偺桳岦僌儔僼偱昞偡偙偲偑偱偒偨丏偙偺恾偐傜偡傋偰偺夝傪媮傔傛丏
丂丂丂偨偩偟丆摨偠憖嶌傪孞傝曉偡夝偼彍奜偡傞丏
丂丂(0,0) (4,0) (1,3) (4,3) (0,3) (3,0) (3,3) (4,2) (0,2) (2,0)
丂丂(0,0) (4,0) (4,3) (0,3) (3,0) (3,3) (4,2) (0,2) (2,0)
丂丂(0,0) (4,0) (1,3) (1,0) (0,1) (4,1) (2,3) (2,0)
丂丂埲壓徣棯 |
2.2丂悈嵎偟栤戣偺夝偼暋悢懚嵼偡傞丏偦傟傜偺側偐偱憖嶌偺悢偑嵟傕彮側偄夝乮嵟揔夝乯傪媮傔傛丏
| 丂丂(0,0) (0,3) (3,0) (3,3) (4,2) (0,2) (2,0) |
2.3丂夝偑擇偮埲忋偁傞傛偆側柪楬栤戣傪嶌傝丆廲宆扵嶕朄偲墶宆扵嶕朄偱夝偄偰傒傛丏廲宆偁傞偄偼墶宆扵嶕朄偱偼栤戣偵傛偭偰偼嵟揔宱楬偑摼傜傟側偄応崌偑偁傞偙偲傪妋偐傔傛丏
丂椺偊偽丆師偺傛偆側柪楬栤戣傪峫偊偰傒傛丅墶宆扵嶕偱偼嵟揔宱楬偑摼傜傟傞偑丆廲宆扵嶕偱偼摼傜傟側偄丅
丂丂丂丂
亙廲宆扵嶕亜
丂丂丂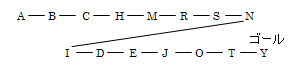
亙墶宆扵嶕亜
丂丂丂
|
2.4丂杮彂偱弎傋偨廲宆扵嶕朄偼偦偺傑傑偺宍偱偼悈嵎偟栤戣傗8僷僘儖傪夝偔偙偲偼偱偒側偄丏側偤側傜偽丆偙傟傜偺栤戣偵偼柪楬栤戣偺傛偆側峴偒巭傑傝偑側偄偨傔塱媣偵怺偔扵嶕偟偰偟傑偆偐傜偱偁傞丏偙偺栤戣揰傪夞旔偡傞偨傔偵廲宆扵嶕朄傪彮偟廋惓偟偨廲宆斀暅怺壔朄乮depth-first
iterative-deepening乯偲偄偆扵嶕朄偑偁傞丏偙傟傜偵偮偄偰挷傋丆偦偺梫揰傪傑偲傔傛丏
| n = 1, 2, 3, 丒丒丒 偲偟偰丆怺偝 n 傑偱偺廲宆扵嶕傪僑乕儖偑尒偮偐傞傑偱孞傝曉偟幚峴偡傞曽朄偱偁傞丅怺偝嵟彫偺夝傪彮側偄儊儌儕徚旓偱尒偮偗傞偙偲偑偱偒傞丅 |
2.5丂師偺扵嶕栘傪嵟椙桪愭扵嶕朄偲嶳搊傝朄傪梡偄偰夝偒丆椉幰傪斾妑偣傛丏
丂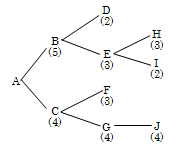 |
丂丂丂丂亙嵟椙桪愭扵嶕朄亜丂丂丂丂丂丂丂丂丂丂丂丂丂丂亙嶳搊傝朄亜
丂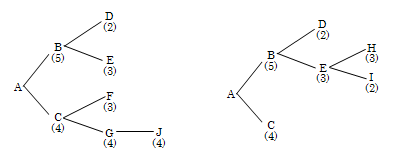
|
2.6丂敪尒揑扵嶕朄偵偼丆杮彂偱弎傋偨曽朄埲奜偵丆價乕儉扵嶕朄乮beam search乯丆斀暅怺壔俙仏傾儖僑儕僘儉乮iterative-deepening A* algorithm乯側偳偑偁傞丏偙傟傜偵偮偄偰挷傋丆偦偺梫揰傪傑偲傔傛丏
丂價乕儉扵嶕朄偲偼丆A仏傾儖僑儕僘儉偵偍偄偰丆揥奐偝傟偰偄側偄愡揰傪慡偰曐懚偡傞偺偱偼側偔丆堦掕悢乮價乕儉暆乯偺嵟椙愡揰偺傒傪曐懚偡傞曽朄偱偁傞丅巊梡儊儌儕偺憹戝傪杊偘傞偑嵟揔夝偼曐徹偝傟側偔側傞丅價乕儉暆傪侾偲偡傞偲嶳搊傝朄偲摨偠側傞丅
丂斀暅怺壔A仏傾儖僑儕僘儉偲偼丆A仏傾儖僑儕僘儉偵偍偄偰丆敪尒揑娭悢偺抣偑偁傞鑷抣乮偟偒偄抣乯埲忋偵側偭偨愡揰偺愭偺扵嶕傪拞巭偡傞傛偆偵偟丆僑乕儖偑尒偮偐傞傑偱鑷抣傪彊乆偵戝偒偔偟偰偄偔曽朄偱偁傞丅 |
2.7丂俙仏傾儖僑儕僘儉傪梡偄偰8僷僘儖傪夝偔応崌丆師偺恾偺尰嵼忬懺 p 偺昡壙抣 f(p)
傪 2.4.2崁 偱弎傋偨曽朄傪梡偄偰媮傔傛丏
 |
丂h(p) = 0+2+0+1+1+0+0+1 = 5
丂f(p) = g(p)+h(p) = 3+5 = 8 |
2.8丂師偺僎乕儉栘偵懳偟偰丆儈僯儅僢僋僗朄偍傛傃傾儖僼傽丒儀乕僞朄偱扵嶕偟偨応崌偺扵嶕夁掱偲寢壥傪愢柧偣傛丏
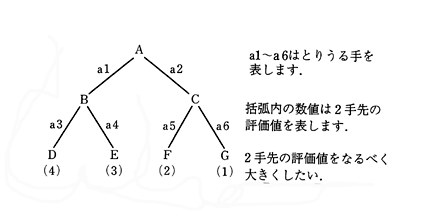 |
丂 |
戞俁復
3.1 恾3.4偺儃乕儖搉偟僾儘僌儔儉偵偍偄偰丆摨恾(b) 偺弶婜忬懺傪師偺傛偆偵曄偊偰幚峴偟偨応崌偺悇榑夁掱傪恾3.5偵側傜偭偰彂偗丏
丂丂1: (person 丱name shiro 丱has nil)
丂丂2: (person 丱name saburo 丱has ball)
丂丂3: (person 丱name jiro 丱has nil)
丂丂4: (person 丱name ichiro 丱has ball)
| 儖乕儖偼丆r1, r3, r2 偺弴偵敪壩偡傞丅嫞崌廤崌偼丆{ (r1,4,3), (r3,2,1) },
{ (r3,2,1) }, { (r2,6,7) }, { } 偲曄壔偡傞丅WM 偺曄壔偼徣棯偡傞丅 |
3.2 恾3.6偱偼儖乕儖r2偲r3傪徣棯偟偰偄傞偑丆偦傟傜偺儖乕儖傪幚嵺偵彂偗丏
(p r2 (person ^name jiro ^has {<x> <> nil } )
丂丂丂 (person ^name saburo ^has nil)
丂--> (modify 1 ^has nil)
丂丂丂 (modify 2 ^has <x>))
(p r3 (person ^name saburo ^has {<x> <> nil } )
丂丂丂 (person ^name shiro ^has nil)
丂--> (modify 1 ^has nil)
丂丂丂 (modify 2 ^has <x>)) |
3.3 嫞崌廤崌CS偑師偺傛偆側応崌丆OPS5偺LEX愴棯偱偼偳偺僀儞僗僞儞僔僄乕僔儑儞偑慖戰偝傟傞偐丏偨偩偟丆儖乕儖偼ra, rb, rc偺弴偵彂偐傟偰偍傝丆偦傟傜偺忦審偺偒偮偝偼偡傋偰摨偠偱偁傞傕偺偲偡傞丏
丂 (a) CS =乷(ra 2 3), (rb 4 3), (rc 2 4)乸
丂 (b) CS =乷(ra 2 4),(rb 4 1), (rc 2 4)乸
丂(a) (rb 4 3)
丂(b) (ra 2 4) |
戞係復
4.1 師偺傛偆側抦幆傪堄枴僱僢僩儚乕僋偍傛傃僼儗乕儉傪梡偄偰昞尰偣傛丏
丂丂丂嘆 僺乕僐偼僇僫儕儎偱偁傞丏
丂丂丂嘇 僇僫儕儎偼捁偱偁傞丏
丂丂丂嘊 捁偵偼梼偑偁傞丏
丂丂丂嘋 僇僫儕儎偺怓偼墿怓偱偁傞丏
丂丂丂嘍 僺乕僐偼1嵨偱偁傞丏
丂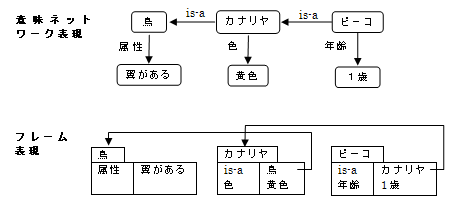 |
4.2 恾4.1偺堄枴僱僢僩儚乕僋偵懳偟偰丆師偺傛偆側幙栤傪昞偡幙栤僱僢僩儚乕僋傪嶌傝丆晹暘徠崌朄傪揔梡偣傛丏
丂丂丂嘆 僠儚儚偺恖婥偼壗埵偱偡偐丏
丂丂丂嘇 僠儚儚偺惈奿偼恖側偮偙偄偱偡偐丏
丂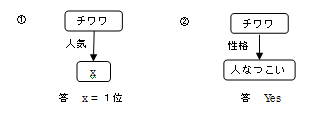 |
4.3 島媊幒C32傗C33偼C搹偵偁傝丆C搹傗D搹偼戝妛晘抧偵偁傞偙偲傪丆僼儗乕儉傪梡偄偰昞尰偣傛丏
丂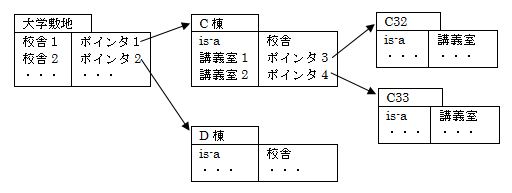 |
戞俆復
5.1 塸暥"The apple is red."傪丆柦戣榑棟偍傛傃弎岅榑棟偱婰弎偣傛丏
丂柦戣榑棟丗 p
丂弎岅榑棟丗佂x [ apple(x) 仺 red(x) ] |
5.2 師偺儁傾偼扨堦壔壜擻偐丏壜擻側傜偽偦偺偲偒偺曄悢戙擖傪媮傔傛丏
丂丂丂偨偩偟丆x, y, z 偼曄悢偲偡傞丏
丂丂丂嘆 p(x, orange) p(apple, y)
丂丂丂嘇 p(x, y) q(z)
丂丂丂嘊 p(x, y) p(q(z), r(y))
丂嘆 x = apple, y = orange
丂嘇扨堦壔晄壜擻 乮弎岅偑堎側傞偨傔乯乯
丂嘊扨堦壔晄壜擻 乮y = r(y) = r(r(y)) = r(r(r(y))) = 丒丒丒丂偲側傞偨傔乯 |
5.3 師偺榑棟幃傪愡宍幃偵曄姺偣傛丏偨偩偟丆x, y, z 偼曄悢偲偡傞丏
丂丂嘆 佂x佂y佂z [(p(x, y) 伻 q(y, z)) 仺 r(x, z)]
丂丂嘇 乣佄x getup(Taro, x)
丂丂嘊 佂x [(p(x) 伻 q(x)) 仺 (r(x) 伾 (佄y佂z (s(y, z) 仺 t(x, y) 伾 u(z))))]
丂嘆 乣p(x, y)伾乣q(y, z)伾r(x, z)
丂嘇 乣getup(Taro, x)
丂嘊 乣p(x)伾乣q(x)伾r(x)伾乣s(S1, z)伾t(x, S1)伾u(z)丂丂偨偩偟丆S1偼僗僐乕儗儉掕悢 |
5.4 師偺栤戣傪儂乕儞愡偱婰弎偟丆SNL偵傛傞摫弌偵傛傝夝偗丏
丂丂乽摦暔傪帯椕偱偒傞偺偼廱堛偱偁傞丏廱堛偵側傞偵偼偦偺帒奿偑昁梫偱偁傞丏壴巕偼廱堛偺帒奿傪傕偭偰偄傞丏僞儅偼擫偱偁傝丆擫偼摦暔偱偁傞丏偝偰丆壴巕偼僞儅傪帯椕偱偒傞偩傠偆偐丏乿
丂嘆 乣veterinarian(x1)伾乣animal(x2)伾can-cure(x1, x2)
丂嘇 乣has-qualification-of-vet(x3)伾veterinarian(x3)
丂嘊 has-qualification-of-vet(Hanako)
丂嘋 cat(Tama)
丂嘍 乣cat(x4)伾animal(x4)
丂嘐 can-cure(Hanako, Tama) 丒丒丒丒丒 徹柧偟偨偄柦戣
丂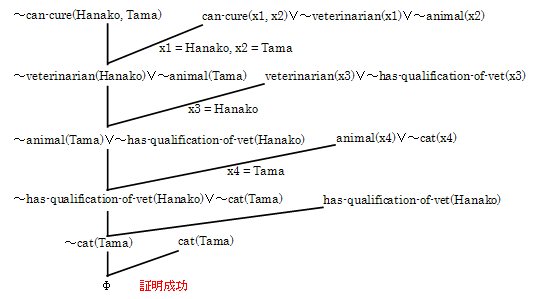 |
5.5 恾5.5 偺僾儘僌儔儉偵偍偄偰恾5.7 偺幙栤偵懳偡傞摎偊偼偳偆側傞偐丏
丂嘆 yes
丂嘇 X = kazuko; X = masakazu
丂嘊 X = masakazu
丂嘋 X = kazuko, Y = ichiro; X = masakazu, Y = ichiro; 丒丒丒埲壓徣棯
丂嘍 X = jiro; X = masakazu
丂嘐 X = jiro |
5.6 乽廸晝乿偍傛傃乽廸曣乿偺掕媊傪Prolog偱彂偗丏
丂uncle(X, Y):-brother(X, Z), parent(Z, Y).
丂aunt(X, Y):-sister(X, Z), parent(Z, Y). |











