４次のRunge-Kutta 法

Vctor クラスとMatrix クラスを導入したことにより，連立常微分方程式

$$\frac{d\mathbf x}{dt} = \mathbf f(\mathbf x)$$ (2.1)

$$\mathbf x(0) =\mathbf x_0$$ (2.2)

を解く４次のRunge-Kutta 法を次のように簡潔に表すことができる．

typedef const vector (vfunc)(const vector&);

// the fourth order Runge-Kutta method
void rk4(vector& x, vector& w, vfunc f, double h)
{
    static  vector kx1, kx2, kx3, kx4;
	
    kx1 = f(x)*h;
    kx2 = f(x+kx1/2)*h;
    kx3 = f(x+kx2/2)*h;
    kx4 = f(x+kx3)*h;
    x += (kx1+2*(kx2+kx3)+kx4)/6;	
}

一方，剛体の無重力状態での運動方程式は右辺に角速度ベクトル 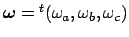$\boldsymbol \omega={}^t(\omega_a,\omega_b,\omega_c)$を含んでいる．すなわち， 運動方程式の右辺はC++で

// system equations
 const vector dxdt(const  vector&  x, const vector& omega)
{
    vector d;
    d[0] = sin(x[2])/sin(x[1])*omega[0] + cos(x[2])/sin(x[1])*omega[1];
    d[1] = cos(x[2])*omega[0] -sin(x[2])*omega[1];
    d[2] = -cos(x[1])*sin(x[2])/sin(x[1])*omega[0] - cos(x[1])*cos(x[2])/sin(x[1])*omega[1] +
         omega[2];
    return d;
}

と表されるので Runge-Kutta 法も次のように修正されなければならない．

typedef const vector (vfunc)(const vector&, const vector&);

// the fourth order Runge-Kutta method
void rk4(vector& x, vector& w, vfunc f, double h)
{
    static　vector kx1, kx2, kx3, kx4;
		
    kx1 = f(x, w)*h;
    w= omega(x+kx1/2);
    kx2 = f(x+kx1/2,w)*h;
    w=omega(x+kx2/2);
    kx3 = f(x+kx2/2,w)*h;
    w=omega(x+kx3);
    kx4 = f(x+kx3,w)*h;
    x += (kx1+2*(kx2+kx3)+kx4)/6;	
}

Runge-Kutta法が実現されれば数値シュミレーションに取り掛かれる．