慣性ロータを用いた倒立振子の姿勢制御
吉住 祐一 楠橋 伸樹 満生 直之
1.諸言
倒立振子とは振子を逆さに立て、バランスをとり倒立させた振子のことである。本研究では通常用いられるバランスをとる為の制御方法とは違い慣性ロータをもちいた制御を行う。慣性ロータでの制御とは、ロータを回転させたことにより発生する反動トルクを利用して制御する方法である。この慣性ロータを用いたシステムを構成し倒立振子を試作し制御理論の研究を行う。
2.制御概念
緒言で述べたように、本研究での倒立振子は、通常の制御法である振子自体を制御するのではなく、ロータに発生するトルクを制御し、その反作用を利用し振子自体を制御する方法を用いている。
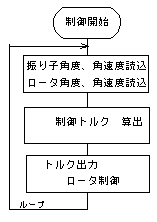 |
図1に制御の流れを示す。まず、振子に取り付けられたセンサで傾斜角度φ2、角速度φ2’を検出。続いてロータの回転角度φ1、角速度φ1’を検出。それらの値をAD変換ボードにより、アナログ信号からデジタル信号に変換し、パソコンに取り込む。パソコンでそれらの値と目標値を比較させ、それに応じたトルクを演算、DA変換ボードによりデジタル信号からアナログ信号に変換、制御回路に出力、ロータにトルクを発生させる。それらの仕事を周期させ制御する。
|
図1.制御の流れ
3.制御装置
制御の流れに示すように、装置は各変位を読み取るセンサ、計算を行うパソコン、トルクを発生させるロータ、電流制御回路で構成されている。
3.1 振子傾斜角度の検出
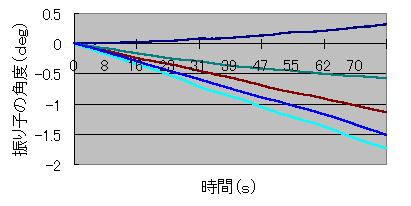
角度を計測するために圧電振動ジャイロを使用する、このセンサは振動体に回転速度が加わるとコリオリ力が発生するという原理を応用した角速度センサである。角度φ2を算出するには、角速度φ2’を時間積分する、しかし、計測を始めると静止しているのに図2の様に角度φ2がずれて残ってしまう(零点ドリフトという)現象が起こる。本実験では外部からの角度計測を行わずに自立して角度を計測できるようにするのが目的であるがまだこれが解決できていないので今後の課題である。
 |
|
| 図2.静止時におけるジャイロセンサの零点ドリフト ※データ数5回分 |
3.2 ロータ回転角の検出
ロータの回転角φ1はロータに取り付けられたセンサ用のモータによって検出される。これはモータの発電が回転数に比例していることを利用したセンサとなっており、この発電電圧から回転角度φ1、角速度φ1’を検出している。
● 制御計算
倒立振り子が安定して倒立し続けるには、常にロータから最適なトルクを発生させバランスを保たなければならない。よって倒立制御するためには、振り子の倒立運動から運動方程式を導き、さらに制御系を安定させることによって、常に安定した倒立ができるトルクT 式を導く。
 |
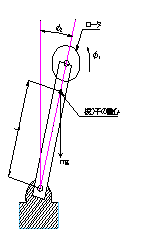 |
φ1:ロータの角度
φ2:振り子の角度 L:回転軸から振り子までの距離 m:振り子の総重量 g:重力加速度 |
図3. 倒立振り子図
図3の簡略図より運動方程式を導くと、ロータから発生するトルクT は、
![]() ……・(1)
……・(1)
となり、このときのJ1はロータの慣性モーメントで、φ1'' はロータの回転角加速度である。また振り子全体の力の釣り合いは、
![]() ・・…・(2)
・・…・(2)
となり、このときのJ2は振り子全体の慣性モーメントで,φ2'' は振り子の回転角加速度である。式(1)、(2)から特性方程式を導き、制御系が安定するよう解を解くとトルクT の式は、
![]() ・・・…(3)
・・・…(3)
となり、このときの k1,k2,k3,k4は角変数の係数、φ1' はロータの回転角速度、φ2' は振り子の回転角速度を表している。この式(3)を用いセンサからの数値を代入して、振り子の位置、状態に適したトルクを計算し、振り子やロータを安定させる。
3.4 ロータに発生するトルク
ロータに発生するトルク、ひいては振子にかかる反動トルクを制御するにはDCサーボモータに流す電流を制御してやればよい、これはDCモータのトルクが電流と比例関係にあるためで、電流を制御することによりトルクを制御することができる。随時変化する逆起電力に対応するため電流制御にはフィードバック回路を用いる。この電流制御回路はDA変換ボードから出された電圧に比例した電流に増幅し、ロータにトルクが発生する。 図4.は回路に流す電流とロータが発生するトルクとの関係を表した。
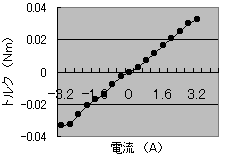 |
図4. 電流とトルクの関係
4.制御実験
4.1 安定状態での制御
倒立を行う前に、安定状態である。普通の振子の制御である。制振を行う、制振とは振子の振幅を制御することで、安定状態で制御理論、各センサ、回路のテストを行う。図5が制振を行った結果になる。
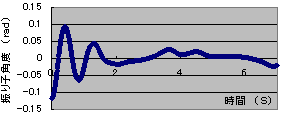 |
図5. 減衰制御時の角度変化
このように、図.6の自由振幅のグラフと比べると分かるように、制振を行った方は振子の傾斜角度φ2、角速度φ2’を強制的にゼロ度地点に持っていく力がしっかりと働いている。このことから自然減衰ではなく、制御されたものだといえる。
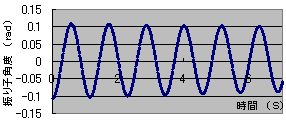 |
図6. 自由振幅での角度
4.2 倒立制御
図7.が倒立制御を行ったときのグラフとなっている、不安定状態の制御ではロータの力不足により制御範囲は狭くなり、制御範囲をこえると制御できなくなるものの、図.7の図に示すように、制御を開始して突然外力をくわえても振子の傾斜角度φ2、角速度φ2’もゼロ点に収束し、ロータの回転角度φ1、角速度φ1’も図8.に示すよう時間がかかるがゼロ点に収束しており、2変数の制御、振子の傾斜角φ2、ロータの回転角φ1を0点に保持する制御で倒立ができていることになる。
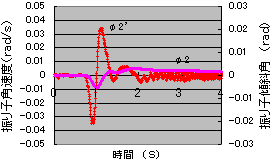 |
図7. 振子の傾斜角度の変化
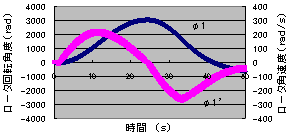
図8. ロータ回転角度の変化
5.結言
慣性ロータを用い倒立振子の制御に成功したが、今回の実験では振子を土台に固定した形となってしまった、最終的には外部からの測定を行わない、独立系のシステムを構成するために、ジャイロセンサなどのドリフト現象を確実に補正する方法の確立が必要となっている。