学生実験用小型磁力支持装置の研究

99E2066　松岡　伸忠          9832056　鳥井　浩平

[指導院生]　呉　鍾彬　　　　[指導教員]　河村　良行

 

１．緒言

　磁力支持装置は、模型に小型永久磁石を内蔵させて、磁力装置に設置されたコイルと永久磁石の間に磁力が発生し、磁場を制御することで、模型に運動を与えることができる装置である。

　今回は、小型磁力支持装置を用いてフィードバック制御を学習する為、学生実験用にZ軸（鉛直方向）制御の小型磁力支持装置を製作した。Z軸制御での臨界制動条件及びステップ応答について計算、実験計測する。

 

２．小型磁力支持装置構成

　小型磁力支持装置の構成をFig.1に示す。パソコン（PC)、電源装置、電流制御装置、空芯コイル（外径180mm、内径140mm、厚さ20mm、巻き数255回、インダクタンス6.89mH）、大型永久磁石（直径60mm、厚さ20mm、表面磁束密度530mT）、小型永久磁石（直径30mm、厚さ10mm、表面磁束密度520mT）×2、浮上模型（重さ48.6g）、位置検出器から構成されている。

装置上部にある大型永久磁石の磁力は、模型に作用する重力と釣り合うようになっており、その位置では浮上模型に力がかかっていない状態となっている。コイルは、位置制御の力を発生させている。

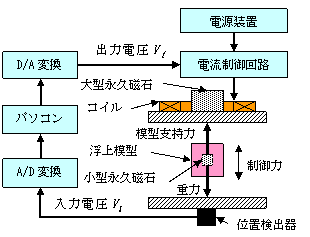
Fig.1　小型磁力支持装置構成図

 

３．制御概要

　３．１　制御方法

　模型支持の制御は以下のように行われる。

（１）          支持装置下部にある位置検出器で模型の位置を検出し、位置に応じて位置検出器から出力される電圧をパソコンに入力。

（２）          位置検出器からの位置電圧を数値のデジタルデータに変換。

（３）          入力された模型の位置データに基づいて計算。

（４）          計算結果の数値データを電圧に変換し電流制御装置へ出力。

（５）          パソコンから出力された電圧に応じて、電流制御装置がコイルへ電流を流す。

（６）          コイルに電流が流れ、コイルと模型内の磁石との間に磁力が発生する。

これらの仕事が6msecの周期で繰り返し行われ、磁力支持の制御が行われる。周期制御プログラムのフローチャートをFig.2に示す。

 

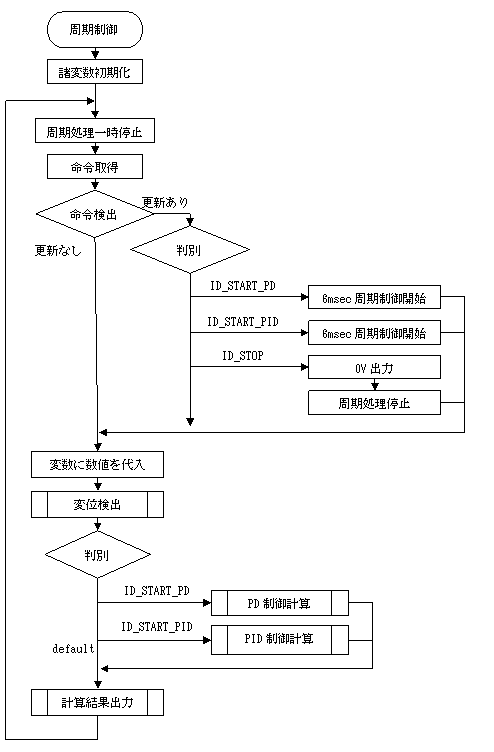
Fig.2　制御プログラムフローチャート

 

　３．２　制御パソコンの基本ソフト選定

　制御プログラムはC++で記述し、基本ソフトはリアルタイムで動作するRT-Linuxを用いた。装置製作の初期段階では、Windows上のVisual C++で磁力支持制御を行ったが安定して浮上させることができなかったため、パソコンに波形を入力し、そのまま出力したときの波形の違いで基本ソフトの性能比較を行った。Windows制御とRT-Linux制御の比較図をFig.3.4に示す。

Fig.3　Windows制御波形　　Fig.4　RTLinux制御波形

（上側）DA出力波形（下側）AD出力波形

1div：縦軸１V、横軸20msec

 

Windowsで10msec周期以下の制御ができないため、10msec以下の数ミリ秒から数十マイクロ秒周期の制御が可能であるRT-Linuxで磁力支持制御を行った。その結果、模型を安定して浮上させることができたため、基本ソフトはRT-Linuxに決定した。

 

４．ステップ応答

４．１　理論計算

ステップ応答を用いて、実験での臨界制動の値(ｋ₂)を求め、臨界制動値の他に、さまざまな値を入力させて、どのようなステップ応答になるかRT-Linuxで実験を行った。

理論値では、出力電圧(V)−距離(m)の比例乗数をAとし、コイルに発生する力Ｆ−コイルにかかる電圧V_fの比例乗数をBとする。V₀は目標値での出力電圧、V_１は位置検出器から出力される電圧、ｋ_１は目標値に対する復元力として以下の式で求まる。

 

 

上の式より、k_１=15となった。模型の重さをm=0.16，A=100，B=0.264の時に、ｋ_２は以下の特性方程式で導かれる。

ｍｓ^２−ｋ_２ＡＢｓ＋ｋ_１ＡＢ＝０

臨界制動条件は、Ｄ＝０の負の重根なので

Ｄ＝（ｋ_２ＡＢ）^２−４ｍｋ_１ＡＢ＝０　

 

 

となる。計算した結果、ｋ_２＝−0.603となった。

模型を1mm動かした時に、電圧は110mV出力される。本来ならば、電圧100mV出力されなければならないが、ＰＤ制御では、外乱などの影響により、目標値の+10％多く出力される。

実験での不足制動(k₂=−0.175)と臨界制動(k₂=−0.4)をグラフ化したものをFig.5　�@と�Cに示す。

４．２　ラプラス逆変換

実験の波形を理論的に求める為、ラプラス逆変換で理論曲線を導いた。ブロック線図を用いた結果、出力Ｖ(s)は、以下の式となる。

 

 

 

臨界制動値(k₂)によって、ラプラス逆変換の式も変わる。k₂の値が−0.175〜−0.6までは、式(1)を

 

 

の式に置き換えてラプラス逆変換すると、以下の式となる。ωは固有各周波数、ζは減数係数とする。

 

 

 

K₂の値が−0.65以上の時は、(1)の分母を因数分解してs(s-α)(s-β)とする。α,βは因数分解した解であり、部分分数分解すると、次の式が成り立つ。γは、(1)の分子であり、x₁,x₂,x₃は定数とする。

 

 

(2)の式をラプラス逆変換すると、

 

となる。

ラプラス逆変換の不足制動(k₂=−0.175)と臨界制動(k₂=−0.6)の波形をグラフ化したものをFig.5　�Aと�Dに示す。

４．３　数値解析

　4.2で求めた方法の他に、数値計算でも理論曲線を求めることが出来る。数値解析では、以下の式で求められ微分には、差分法を用いている。

 

　

　数値計算では、微分方程式で表すので、(3)の式を出力電圧から変位(位置)に変えて計算すると以下の式となる。

 

 

数値解析の不足制動(k₂=−0.175)と臨界制動(k₂=−0.55)の波形をグラフ化したものをFig.5　�Bと�Eに示す。

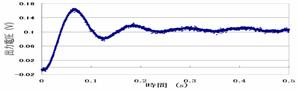
�@実験　不足制動　ｋ_２=-0.175

 

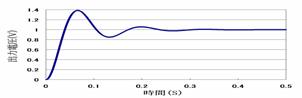
�Aラプラス逆変換　不足制動　ｋ_２=-0.175

 

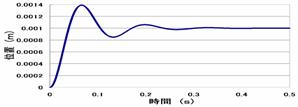
�B数値解析　不足制動　k₂=-0.175

 

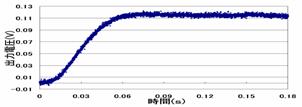
�C実験　臨界制動　k₂=-0.4

 

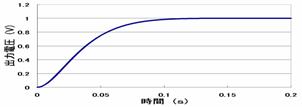
�Dラプラス逆変換　臨界制動　ｋ_２=-0.6

 

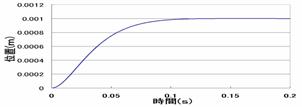
�E数値解析　臨界制動　ｋ_２=-0.55

 

Fig.5 ステップ応答

 

５．結言

·  制御実験を行った結果、RT-Linuxが一番安定していた。

·  臨界制動係数(k₂)を−0.9以上すると、立ち上がり時間が遅くなり、収束しても不安定なままであった。

·  ラプラス逆変換と数値解析の２種類の理論曲線を導き、ほぼ実験データに近い波形が出せた。