研究室メンバー紹介
MENU
溝田研究室
日本風工学会誌 第６２号 平成７年１月
第１報 準定常理論による飛翔解析とフラッター実験
Erratic Behaviour of Knuckleball
(1)Quasi-Steady Flutter Analysis and Experiment
福岡工業大学 工学部 電子機械工学科 溝田武人
福岡工業大学大学院 工学研究科 電子機械工学専攻 久羽浩幸
金沢大学 工学部 機械システム工学科 岡島厚
1．はじめに
各種のｽﾎﾟｰﾂに関する力学の中でその面白さが流体力学に起因する問題は数多くある．硬式野球ボールの変化球の一つにナックルボールと称する魔球がある．アメリカ大リーグのメジャーリーグでも現在2・3人しか投げていない特異なボールである．指の第一関節(Knuckle)を使って投げるのでこの呼称の由来があるが，特徴は超スローボールであること，ボールの回転が少ないこと，そしてとりわけ飛翔中にゆらゆらと揺れてホームベース付近で大きく変化することにある．ボールの握り方が違っ ていてもこのような変化球を投げる投手はいる．
ナックルボールに関するこれまでの研究1)によると，ボールの回転により縫い目位置が変化し，それによって回転軸に直交方向に空力特性が正負に変化するので，その結果ボールの振動挙動が生じる，と説明されている．そしてゆらゆらと揺れるボールの2次元挙動に関して計算が行われ，文献2)，3)でも紹介された．
しかしながら，これまでの研究では，ナックルボールの3次元的な挙動や，縫い目位置や流れのレイノルズ数の変化にともなう空力3分力特性の系統的変化については明らかにされているとは云えない．またナックルボールの変化に関する実験的な 裏付けも行われていない．縫い目位置とまわりの流れおよび作用する空気力の関係は分かっていない．ここでは，ナックルボールの不思議な飛翔軌跡に関して空気力学的な手法によってさらに解明を試みる．その結果を，以下のように2報に分けて報告する．
第１報では，まずテレビ放映のスーパースロー画像4)からナックルボールの軌跡と回転速度および回転軸方向を観察した結果を報告する．続いて，風洞実験によって硬式 野球ボールに加わる空力３分力を測定し，準定常性を仮定してボールの３次元飛翔軌跡の方程式を求める．それを解いて，ボール軌跡の振動挙動に関するコンピュータ･シミュレーションを行った．また風洞装置によるフラッタ実験により，振動振幅を測定し，両者が良く一致することを確かめた．この結果，ナックルボールの変化の様相は，ボールのゆっくりした回転に伴うフラッタ現象であることを結論する．
第２報5)では，縫い目位置の変化にともなう，後方のWake fieldの速度欠損領域，およびボール表面の境界層の層流から乱流への遷移，それにともなう剥離点の後退などの流れの様相変化を求め，ボールのゆっくりした回転にともなう抗 力変化と大きな横力変化の発生のメカニズムを明らかにした．また，ボールに加わるトルクについても考察した．
２．記 号
第1報，第2報で使用した主要記号を以下のように定めておく．
Ａ ：一様流に垂直な面への野球ボールの投影面積，
：X方向時間平均抗力，Y方向時間平均揚力，Z方向時間平均横力
：変動抗力，変動揚力，変動横力，
：時間平均抗力係数，時間平均揚力係数，時間平均横力係数，
：変動抗力係数，変動揚力係数，変動横力係数，
：
，
：
，
：
，
：
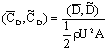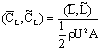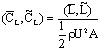のY方向成分，（γだけ傾けた場合）
：のZ方向成分，（γだけ傾けた場合）
N ：ボールの回転速度，rps
Re ：レイノルズ数，
，
：投手の手を離れたボールの初速度，
U ：ボールスピードあるいは一様流の流速，
：ボール回転にともなう無次元流速，
，
d ：ボールの直径，d=φ0．0715m，
g ：重力加速度，
m ：硬式野球ボールの質量，m=144．5gr，
t ：時間
α ：ボールの投げ上げ角度，
γ ：X軸まわりのボールの回転角度，
θ ：Y軸まわりのボールの回転角度，
ρ ：空気密度，
ν ：作動空気の動粘性係数．
３．風洞およびフラッタ実験装置
実験に使用した風洞は，福岡工業大学電子機械工学科に設置してある0．40m
×0．40mの吹き出し部を有する小型・低速風洞6)である．吹き出し部の流速は0～44m/s(0～158．4Km/h)，風洞気流中央部の乱れ度は0．1%以下であるが，測定部を開放型としてこの実験を行っている．ボールに加わる空気力の測定は，3分力
測定用のﾛｰﾄﾞｾﾙを利用した．Fig．1に風洞吹き出し部とボールの設定状況を示す．一様流の方向を+X，上方を+Y，+Zを図のような方向とする．X，Y，Z方向の時
間平均的及び変動空気力をそれぞれ抗力
，
，揚力
，
，横力
，
とし，抗力係数
，
，揚力係数
，
，横力係数
，
を，２．記号
の中に記述したように定義する．なおFig．1では後方からボール支持を行っている様子を示しているが，ボールを回転させる場合は下方から支持する．その場合は，φ6mmの支持棒に加わる力を差し引いている．
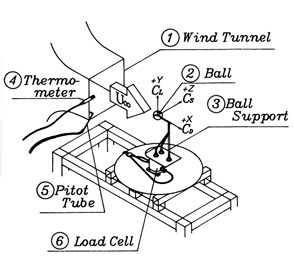
Fig.1 Wind tunnel experimental apparatus.
野球ボールの回転にともなう振動挙動を調べるフラッタ実験では，Fig．2のように２本のレールに摩擦の少ないベアリングﾞを介して載せた移動台の上で，野球ボールをゆっ くりと回転させ，横力の作用によってボールと移動台が振動変位する様子を調べ る．振動変位は移動台の壁面に光を当てたレーザー変位計によって測定した．フラッタ 実験装置を風洞の計測部にセットした状況をPhoto．1に示す．写真左側にレーザー変位計が見える．
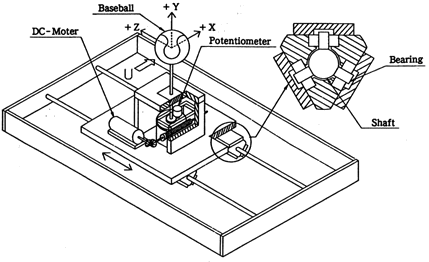
Fig．2：Experimental apparatus for measuring oscillating amplitude of baseball
(左）Photo.1 Wind tunnel and apparatus for
flutter experiment.
(右）Photo.2 Streakline around baseball by smoke-wire method.
野球ボールの縫い目位置を，Fig．3(a)，(b)，(c)に示すように定義する． Fig．3(a)θ=0°のTop viewは+Y方向から見たボールの縫い目の配置であり，風洞 実験の一様流の方向は-Xから+Xに向かっており，キャッチャーは-X方向から見ている ので，Catcher viewと称する．Top viewの+Y軸(Fig．1参照)を中心にして時計 方向に35°および45°回転した配置がFig．3(b)θ=35°(c)θ=45°である． Photo．2にスモークワイヤー法によってθ=0°の縫い目配置の野球ボールまわりの流跡線 を求めた例を示す．この例はレイノルズ数が低い(Re～3．9×103)ので，第2報で述べるナックルボールのレイノルズ数Re～105の流れとは剥離位置などが異なっているが， 流れの様子はつかめる．
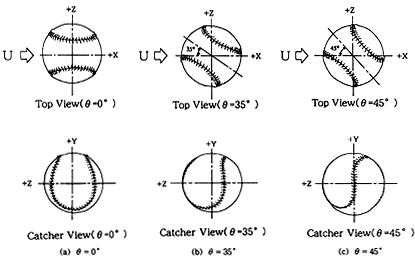
Fig．3(a)，(b)，(c)：Definition of seam position，
４．ビデオ画面の観察
アメリカ大リーグPittsburgh Piratesの1992年の新人投手 Wakefieldの手を離れて ホームベース付近まで来たナックルボールのビデオ映像4)から撮ったスチール写真の一部を Photo．3(a)，(b)に示す．またボールの回転の様子を転写してFig．4に示す．カメラの位置はバックネット付近右打者後方で打者の眼とほぼ同一の高さにある．ただし， 転写の時間間隔は同一ではない．この画像および音声情報から，以下のデータをまとめておく．
(a) (b)
Photo.3 (a),(b) Knuckleball by Wakefield 4)
(View from a right-handed batter)
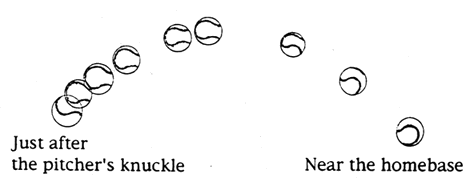
Fig.4 Knuckleball trajectory and rotation traced from TV pictures4).
(1)ボールの初速は，U=76Km/h(21．1m/s)である．いわゆる大リーグボールの 1/2程度のスピードしかない．投球板とホームベースの間隔は18．44mであり， 滞空時間は約0．88Sとなる．
(2)ボールは飛行中にわずか90°ﾊﾞｯｸｽﾋﾟﾝした．したがって，ボールの回 転速度はN≒0．284rpsである．
(3)レイノルズ数はRe≒105であり，滑面球では亜臨界域のレイノルズ数であるが， ボールの（縫い目位置の盛り上がりの高さ1mm）/（直径d）≒0．013はトリップ・ワイヤになっており，しかもその位置は一様流がボールに当たる 表面上で複雑に変化する．ボール表面の境界層は層流剥離あるいは乱 流剥離の両者が混在する，と予想される．
(4)ボールの回転速度Nに基づく無次元流速は，=1038．8となり，空気力は準定常的に作用していると考えられるが，ボール回転にともなっ
て層流剥離，乱流剥離のヒステリシスも発生し得る．
５．野球ボールに作用する空気力の測定
５．１ 滑面球の空力３分力測定
野球ボールに作用する空気力の測定が正しく行われているかどうかを確認する
ために，予め滑面球に加わる空気力を測定した．その結果を，Fig．5に示す． この抗力係数は滑面球に関する亜臨界域でのこれまでの測定結果7)とほぼ等
しい．しかし，実験を行ったレイノルズ数範囲では，まだ臨界レイノルズ数に達していない．
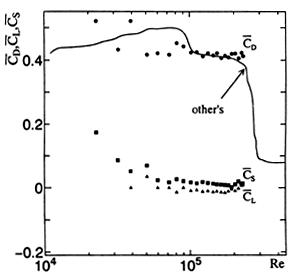
Fig.5 Aerodynamic forces on a sphere of smooth surface.
５．２ 縫い目配置と空力係数
野球ボールの空力特性の横力は縫い目位置の変化で激しく変化することが知られているが1)，抗力，揚力および相互の関係は明確になっていない．ボールの縫い目配置と空力係数の関係を求めるためにボールを5°ずつ回転させて，，を測定した．一様流速U=21．1m/sの場合をFig．6に示すが，ボールが360°，1回転する間に，，は明らかに4周期変化している．，の変化は，縫い目が上下方向に向けて1周4列あることによって説明がつく．縫い目配置が接近流側からみて最大円周上にある45°，135°，225°，315°付近は値が最大になる角度である．
値は0．4から0．7の間で大きく変化している．これは回転にともなって抗力が変化し，その結果ボールスピードの変化を生む原因になる．
値が+Zの方向に最大になるのは，Fig．3(b)の35°，125°，215°，305°付近である．値は0．4～0．7付近で変化するが，値が0．4～0．5にもなりほぼ値に匹敵する値に達することは注目に値する．これらについては，第2報5)で流速分布の測定結果とともに考察する．
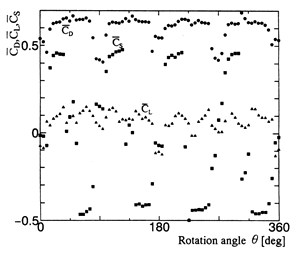
Fig.6
,,
and
values with change of spin angle θ.
(U = 21.1 m/s, 76km/h, Re ≒ 105)
５．３ ボール回転速度に対する横力の準定常性
一様流中に置かれたボールをFig．3のY軸まわりにN=0．22rpsでゆっくりと連続回転させ，ボールの回転角度と横力の関係を出力した結果をFig．7に示す．測定はU=21．1m/s(Re=105)で行い，(a)は横力の生波形，(b)は縫い目位置を示している．ボールの回転方向は，+Y側から見て時計方向である．(b)の縫い目波形のプラス側の最大値は横力が+Z側に最大となるようにセットしている．ボール1回転につき4回の最大値をとる．(a)の横力の生波形の振幅はほぼ=0．4であり，ボールの回転角度θ=90°ごとに最大値となり，ボール1回転につき4周期の変動を示す．
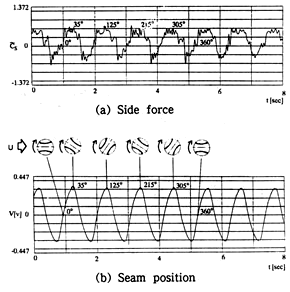
Fig．7：Wave form of (a)side force and(b)seam position．
Maximum values of the signals of wave(b) coincide with the seam position θ=35°． Spin rate N of the baseball is 0．22rps．
つぎに，ボール回転速度をN=0～0．8rpsと変化させ，変動横力係数と縫い目位置35°との位相関係φをまとめた結果をFig．8に示す．測定範囲ではほぼ=0．4であり，位相もφ=0°付近を示している．ゆっくりした回転にともなう縫い目位置の変化と横力の変動振幅の位相関係は，空気力の準定常性が成立することを示している．
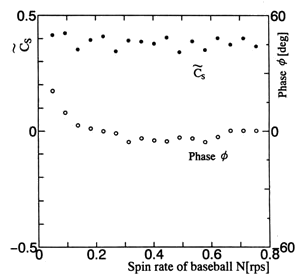
Fig．8：Oscillation amplitude of side force
coefficient
and phase angle φ with the change of spin rate N of the
baseball．
しかしながら，ボールのゆっくりした一様回転にもかかわらず，回転方向に応じて，回転にともなう変動横力()と同時に時間平均的な定常横力()が作用することが分かった．Fig．7の生波形は+側にシフトしていることからもこのことが分かる．ボールを+Y側からながめて時計方向(CW)，および反時計方向(CCW)に
ゆっくりと回転させた場合の定常横力を15，20，25m/sの3種類の流速で測定した結果をFig．9に示す．
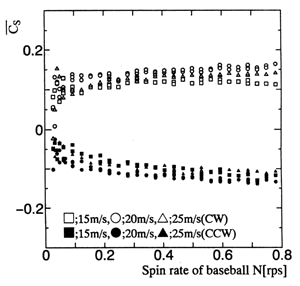
Fig．9：Steady side force coefficient
with the change of spin rate N
この定常横力の作用方向は，いわゆる回転にともなうマグナス効果と同一方向である．このような力の作用はこれまで分かっておらず，準定常空気力では説明できないが，第2報5)で後流の速度分布の測定結果とともに議論する．
５．４ レイノルズ数の影響
野球ボールの空力特性に及ぼすレイノルズ数依存性について縫い目配置を変化させ
て調べたいくつかの実験結果のうち，Re≒105で最大横力が発生するボール回転角度θ=35°の場合をFig．10に示す．横力係数はRe≒105で0．40程度の一定値となった．
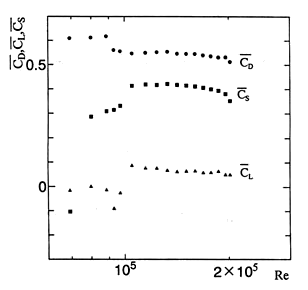
Fig．10 :Dependence of Reynolds number on aerodynamic forces of baseball （θ=35°）
６．ボ－ルの飛翔軌跡
６．１ 飛翔の方程式
空気力の準定常性を仮定するとゆっくりと回転するボールに加わる力の平衡方程式をたてることができる．今ボールがFig．3(a)のCatcher view のY軸(ボールに固定)まわりに回転しながら飛んでいる場合，ボールに作用する空気力として抗力と横力のみ考え，揚力を無視する．しかし，Fig．11のようにボールをX軸（紙面に垂直方向）まわりに
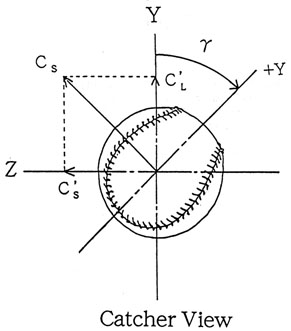
Fig．11 Inclined arrangement of Knuckleball
時計方向にγ°回転させた姿勢で，傾斜した+Y軸のまわりに自転しながら，投手の手を離れてホームベース方向に飛翔する場合には，横力の分力として鉛直Y方向，水平Z方向に空気力
，
が作用し，の分力として，
，
が作用する．しかし，この
γ°の傾斜によって，抗力は変化しない．このような状況で，投球板中央から ホームベースに向かうボールの運動方程式は，
････(4)，
･･･(5)，
････(6)，
となる．γ°の傾斜では
，は
となるので，
(5)，(6)式の係数が決まる．(4)，(5)，(6)の各式で，左辺第１項は慣性力，第２項
はボール自転にともなう変動空気力である．ボールの鉛直Y方向の運動にともなう迎角変化もあるが簡単のためにこれを無視する．Z方向の変化によるボールの迎
角変化による空気力の変化は十分小さいとする．(4)式の第３項は定常抗力であ
る．Fig．9で示した定常横力の分力も無視する．相互の位相関係も省略している．
(4)，(5)，(6)式の初期条件を，
(1)ボールの初速を，
(2)投手は，水平線に対して迎角αでボールを投げる， とする．X，Y，Zは，
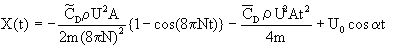･････(7)，
･････(8)，
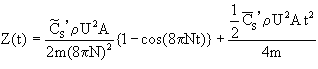･････(9)，
となる．
６．２ 飛翔軌跡の計算
Ｎの値を変化させた計算結果の3例を Fig．12，Fig．13，Fig．14に示す．各図とも(a)は，Top view，(b)はSide view，(c)はCatcher viewである．なお○印はボールの軌跡を表しているがFig．13，Fig．14の変位の変動成分は拡大して表示している．Top view，Side viewに記入した破線は，空気力を受けない時の軌跡を比較のために示した．Catcher viewの地面上に記した破線は，鉛直平行線上からの投影を 地表面上に示した．回転周期の違いによってボールの軌道が種々変化していることがわかる．
実際の投手はナックルボールを投げる際に，投手自身も「どこに行くか分からない」 と言っているが，少なくともストライクゾーンに入るように，ボールの飛翔軌跡をある 程度予測しているものと考えられるので，シミュレーションの過程でも，投げ上げ角度などのいくつかのパラメータを変化させ，試行錯誤の上コンピュータ画面上に表したものである．次のような打者達のいずれもファジイなコメント8)，9)は，Fig．12，13，14の 飛翔模様と各々対応している．
「宇宙遊泳のようだ」， ：Fig．12
「ﾃﾆｽﾗｹｯﾄでもないと打てない」， ：Fig．13
「まるで蝶のようだ」，
「ナックルボールを打つなんて，それは飛んでいる蝿を箸で掴むようなものさ」 ：Fig．14
ただし，この計算では無視したが，Fig．9に示した定常横力のZ方向成分を仮に=0．07とすれば，ホームベースまでの定常変位量は0．17mになる．
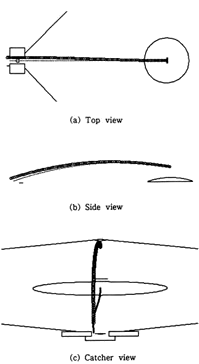
Fig．12 (×1) Knuckleball trajectory
N=0．142rps，α=+10°，γ=45°，=22．5m/s
，=0．55，=0．15，=0．400(==0．283)
(a)Top view (maximum double amplitude :284mm)
(b)Side view
(c)Catcher view
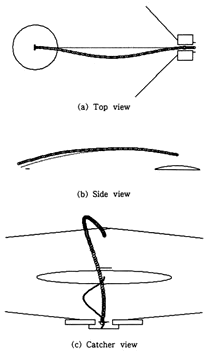
Fig．13 (×10) Knuckleball trajectory
N=0．278rps，α=+10°，γ=45°，=22．5m/s，=0．55，=0．15，=0．400(==0．283)
(a)Top view (maximum double amplitude :83．6mm)
(b)Side view
(c)Catcher view
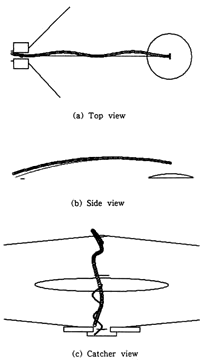
Fig．14 (×20) Knuckleball trajectory
N=0．603rps，α=+10°，γ=45°，=22．5m/s，=0．55，=0．15，=0．400(==0．283)
(a)Top view (maximum double amplitude :19．1mm)
(b)Side view
(c)Catcher view
６．３ 抗力の変化にともなうボールスピードの変化
また，実際に投げられる変化球が打者にとって打ちにくくなる重要な因子に スピードの変化がある．(7)式からボールのX方向スピードdX(t)/dtは，
･････(10)，
となる．したがって，ボール回転にともなって値が0．4から0．7の間で変化する
(=0．15)ことによるボールスピードの変化の幅は，N=0．1rpsの場合0．33m/sになる．
このようにボールスピードの変化率が振動的になれば，平均的なスピードが大リーグボールの1/2程度であっても打者にとってはタイミングを取りにくい魔球になるであろう．
７．Flutter実験による最大振幅の比較
７．１ 最大シフト量の検討
ナックルボールの3次元振動挙動を示す式(7)，(8)，(9)の結果を確認するために，フラッタ実験を行った．ボールの回転軸をFig．3のようにセットし，ボールの振動変位方向を±Z方向のみに拘束する．その場合の振動成分の変位は(9)式のをとし
て，
･･･(11)
となる．以下，Z(t)の最大シフト量をZmaxとする．Zmaxは，ボールが18．44mの ホームベースに達する前に半周期以上が実現するように揺れるかどうかという条件により異なる．すなわち，U=20．6m/sでは，
1) N≧0．139secの場合，
･･･(12)
となる．
2) N＜0．139secでは，(11)式が適用できて，
･･･(13)
となり，極端にゆっくりと回転するN～0の場合は，
･･･(14)
となる．以上の結果は，実験結果と共に次節で示す．
７．２ Flutter実験結果
Fig．2のような摩擦の少ない駆動装置上でボールを回転速度N rpsで回転させ，
ボールを含む駆動装置の振動挙動をレーザー変位形で測定した生波形を，
Fig．15(a)(N=0．40rps)，Fig．16(a)(N=0．60rps)に示す．両図とも(a)が振幅，
(b)は縫い目位置の通過に同期させたポテンションメーターからの信号であって，ボール回転速度Nの4倍の波形である．これらの波形から，全体として大きなゆらぎ状の変位に乗ってボール縫い目の周期と同期した振動が発生していること，ボール回転速度Nが増加すると振動振幅は減少(Fig．15(a)→Fig．16(a))していることがわかる．ただし，実験ではFig．9に示した定常横力を打ち消すように，Fig．2のレールを少し傾斜させている．
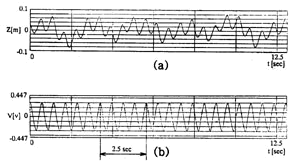
Fig．15(N=0．40rps) (a)Oscillation amplitude of knuckleball， (b)Seam position
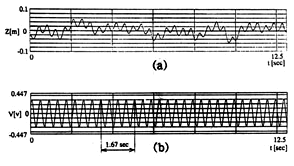
Fig．16(N=0．60rps) (a)Oscillation amplitude of knuckleball， (b)Seam position
これらの波形をFFTアナライザーで解析し，縫い目の周波数(4×N
Hz)に一致する周波数の振動振幅の大きさを求める．式(11)の準定常理論による計算値Zmaxを
実線で，実験値を○印でFig．17に各々示す．ここで，計算値では=0．40としている．なお，振動質量mはボール質量で補正してZmaxを求め，N＜0．139secの実験結果は(11)式で補正して，Fig．17上に示した．
準定常理論と実験結果は良く一致している．低回転速度領域では実験値がばらつくが，これは振動質量が大きいために大きな補正をしているためである． Zmaxはボールの質量mに逆比例し，(11)式に従う回転速度 N≧0．139rpsでは，ボール回転速度Nの2乗にも逆比例する．したがって，ボールの回転速度Nが増加す れば急激に最大シフト量Zmaxは減少する．
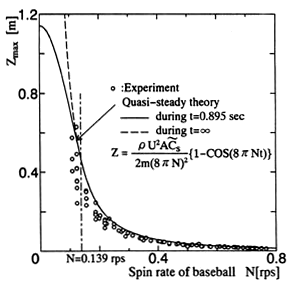
Fig．17：Maximum shift value Zmax
of knuckleball with spin rate N (U=20.6m/s，=0.40，)
８．第1報の結論
ナックルボールの飛翔軌跡をテレビ画面から観測し，準定常空気力を適用した飛翔に関する運動方程式を解いて，種々の変化の様相をコンピュータ･シミュレーションにより求めた．この結果は打者達のボール軌跡のファジーな印象表現と良く対応した．また，ボールのゆっくりした回転速度の変化にともなって変化するナックルボールの振動振幅を準定常理論により求めた．この値は，フラッタ実験の結果と良く一致した．
参考文献