研究室メンバー紹介
MENU
溝田研究室
日本風工学会誌 第６２号 平成７年１月
第２報 硬式野球ボールのWake Fieldと空気力
Erratic Behaviour of Knuckleball
(2)Wake Field and Aerodynamic Forces
福岡工業大学工学部電子機械工学科 溝田武人
福岡工業大学大学院電子機械工学専攻 久羽浩幸
金沢大学工学部機械システム工学科 岡島厚
１．はじめに
前報1)では，テレビ放映のスーパースロー画像からナックルボールの軌跡と回転速度および回転軸方向を観察し，風洞実験によって硬式野球ボールに加わる空力３分力を測 定した結果をのべた．そして，準定常性を仮定してボールの3次元飛翔軌跡の連立方程式を求め，それを解いて，ボールの振動挙動に関するコンピュータ・シミュレーションを行った．また風洞装置によるフラッタ実験により，振動振幅を測定し，両者が良く一致することを確かめた．
ひき続き，この報告では，硬式野球ボールの縫い目位置の変化にともなう，後方のWake fieldの速度欠損領域，およびボール表面の層流境界層，乱流境界層および剥離位置の変化を熱線流速計のI型センサにより求め，考察を行う．
第1報では，ボールの角度θ(第1報のFig.3参照)の変化による縫い目配置によっ て特徴的な空力特性が生じることをのべたが，それをまとめると，
(1)θ=0ﾟ付近で抗力係数が最小になり，
(2)θ=35ﾟでは横力係数が最大値に達し，
(3)θ=45ﾟになると抗力係数がほぼ最大になる，
ということになる．そこで第2報では，これらのボール角度の縫い目配置に注目して，空気力の発生のメカニズムを，流れの変化に基づいて考察する．ボールに作用するトルクに関するコメント2)ついても言及する．
２．野球ボール後方の流速分布
野球ボールの後方のような非定常流速を含む逆流域の時間平均流速を熱線流速計のI型センサで測定する場合には注意が必要である．それは，非定常流速成分が 大きくて正逆両方の流速が混在する領域では，I型センサの出力が物理的に意味のない信号を示すことがあるからである．その点に注意して，以下の測定を行っ た．
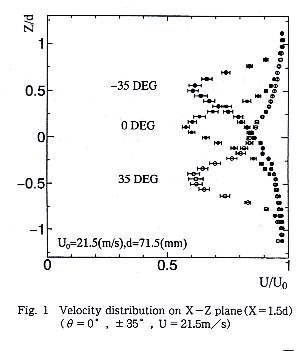
Fig.1はθ=0゜（一様流に対するボール配置はFig.3に示す），±35゜（Fig.4 に+35゜の配置を示す）の場合の野球ボール中心からX=1.5d後方の時間平均流速 と変動流速のRMS値である．変動流速のRMS値は一様流の高々2～3%であった． ボールの角度θ=0゜のこの計測例では後流の中心が少し+Z方向にずれているが， 最大速度欠損はボール背面からわずかに直径倍の所で，すでに60%まで回復して いる．
θ=+35゜の場合，速度欠損領域は大きく-Z方向にシフトしており，流れ場の運 動量の反力として，
=+0.40という大きな＋の横力が作用していることと対応
している．θ=-35゜の場合には+35゜の場合と逆に後流が+Z方向にシフトしている．
なぜ，±35ﾟの場合にこのように後流が大きくシフトするのか，その理由は4章で のべる．
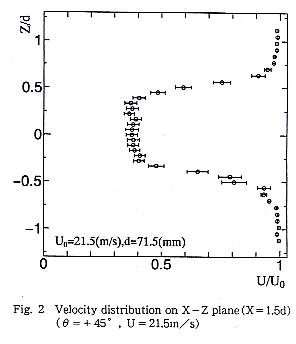
θ=+45゜の場合には，第1報のFig.6に示したように抗力係数
がほぼ最大に
なり，横力係数はほぼ0である．この場合，Fig.1のθ=0゜の場合と比較して，
Fig.2の速度欠損は40%程度しか回復しておらず，欠損領域の幅も広い．これは，
θ=+45ﾟの配置では縫い目がボールの前面のよどみ点位置から90ﾟ近くにあり，そこで流れの剥離が発生しているからである．また横方向にはほとんどシフトして
いない．
３．Wake fieldの再循環領域
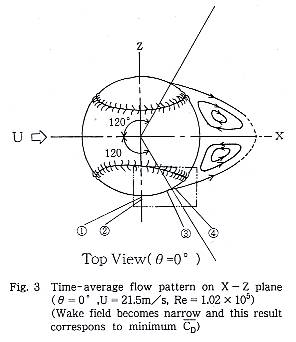
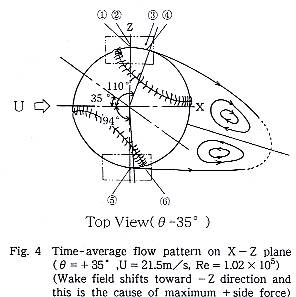
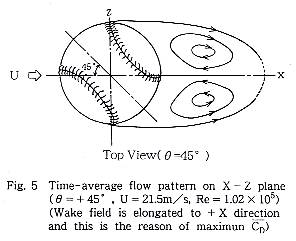
速度欠損の測定と，表面近くおよび剥離せん断層付近8～10ヶ所にわたる流 速測定を基に，θ=0゜,+35゜,+45゜の場合の後流の時間平均的な再循環領域を 定性的に画いた．一様流と再循環領域の境界は，I型センサの出力に剥離せん断層 特有の乱れが生じる位置とした．その結果を，Fig.3，Fig.4，Fig.5に示す． このようにして求めた再循環領域については別に行ったタフト法による実験で確認し，両者の結果はほぼ一致した．その理由は，これらの領域の変動流速成分が一様流の流速の2～3%と小さいことによると考えられる．
Fig.3(θ=0゜)では，再循環領域は狭く，第1報のFig.6に見られたごとく， 抗力係数が低い値になることと対応している．次に，Fig.4(θ=+35゜)で示
すように，θ=+35゜の場合，再循環領域は大きく-Z方向にシフトしている．ボール
をゆっくりと回転させながら，タフト法によって再循環領域をビデオ撮影し，-Z方
向へのシフト量が最大になることを確認した．これらの結果から，θ=+35゜の場
合に横力が+Zの方向に最大になることを説明できる．Fig.5(θ=+45゜)ではよ
り広い再循環領域が上下対称に形成されており，抗力係数の増加と横力が０に
なることが，再循環領域のそれぞれ流れと対応していることがわかる．なお，
Fig.3，Fig.4の2点鎖線で囲った領域の中の番号は次章で説明する流速測定の位置を示す．
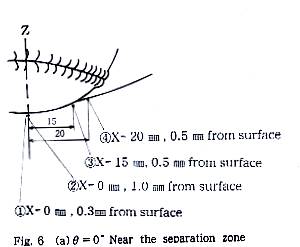
４．ボール表面からの層流剥離・乱流剥離
この章では，ボール表面の境界層付近における流速をI型センサで計測し，その結 果を基に表面境界層および流れの剥離の状況が層流？あるいは乱流？と言うことおよび剥離位置はボールの赤道上のどの位置かという問題を議論する．一様流 速はU=21.5m/sに固定している．ただし，壁面からの距離の計測は十分な精度ではなく，つねに±0.1mm程度の誤差がある.
４．１ θ=0゜の場合
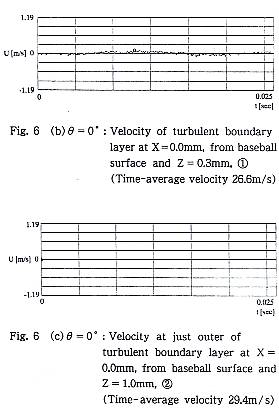
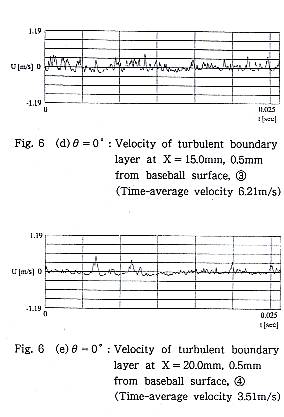
Fig.6(a)にθ=0゜の場合のZ/d=-0.5付近の流速測定位置を示す．壁面近傍① はちょうど-Z軸上であって，わずか0.3mmだけ壁面から離れた位置の流速信号 をFig.6(b)に示す．ここでは，平均流速は26.6m/sを示した．流速の信号は乱 流境界層であることを示している．Fig.6(a)の②に示す位置は壁面から1.0mm の位置であり，Fig.6(c)に示す流速信号の平均流速は29.4m/sであった．ここ では流速の変動振幅は小さくなり，信号はV=0上にほとんど重なっている．乱流境界層の外側の非回転流に位置していると考えられる．Fig.6(d)の信号は， ③の位置であり，X=15.0mm後方で壁面から0.5mmの所であり，時間平均流速は 6.21m/sとなり，乱流境界層として充分に発達していることを示している． Fig.6(e)は④のようにX=20.0mm後方で，壁面から0.5mmの位置では，時間平均 流速は3.51m/sとなり，この位置では早い流速へとスパイク状に変化することから， その前方の壁面で流れは剥離し，測定位置の外側を通る剥離せん断層が間欠的に測定位置に進入していると考えられる．
これらの事実から，θ=0゜の場合の 剥離位置はX軸上の前面淀み点から±120゜付近であると結論される．
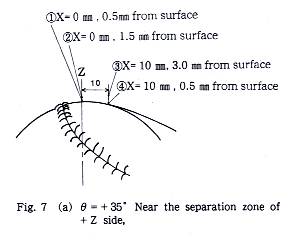
４．２ θ=+35゜の場合
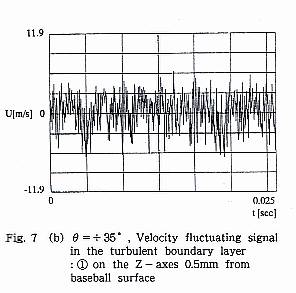
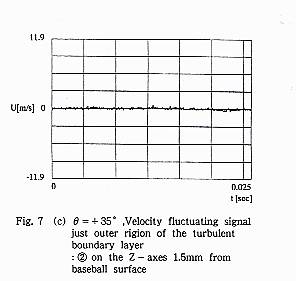
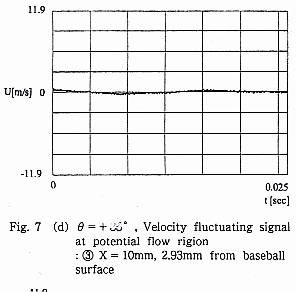
ボール前面から時計方向+90゜付近のFig.7(a)の位置では，表面から0.5mmの① における流速は，Fig.7(b)のように非常に激しい変動を呈しており，明らかに 乱流境界層の信号である．しかし，そこからわずかに+Z方向に1.0mmずれた， 表面から1.5mmの位置②では，Fig.7(c)のように変動振幅は急激に低下し，乱流境界層の外であることを示す．そこから後方X=10mmの位置③では，流速の信 号Fig.7(d)はFig.7(c)とほぼ同一である．表面から，0.5mmの位置④における 流速変動Fig.7(e)はFig.7(b)と同じく，乱流境界層であることを示す．
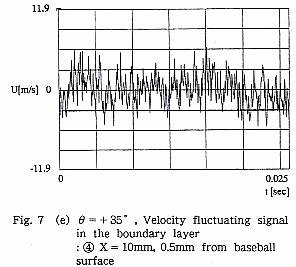
一方，ボール前面から反時計方向-90゜の付近の-Z側剥離位置付近では， Fig.8(a)のように⑤の表面から0.3mmの位置のFig.8(b)に示す信号は，明らか に層流境界層であることを示している．その位置から10.0mm後方で，表面から2.5mmの位置⑥では，Fig.8(c)のように乱流の信号と層流の信号が時間をおいて混在し，境界層が層流剥離し，剥離せん断層は剥離時の層流を保ったり乱流に遷移したりして間欠的に変化することを示す．
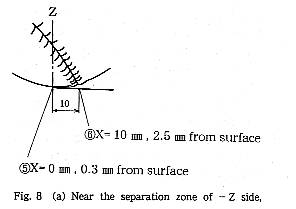
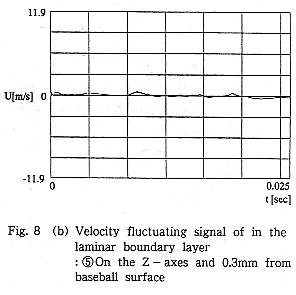
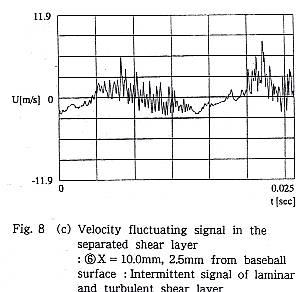
これらの結果から，+Z側の剥離位置は，X軸から時計方向(CW)に110゜付近に あり，乱流剥離である．-Z側の剥離位置は反時計方向(CCW)に約94゜で層流剥 離しているということができる．
ボール角度によってボール表面の縫い目の位置は変化するが，前面淀み点から3
次元的に発達する境界層のどの部分に縫い目（粗さ）があるかによって，境界層が層流から乱流に遷移する位置は変化する．その結果，一方の剥離点の位置
がX方向に大きく後退した場合には再循環領域は-Z側に大きくシフトし，結果とし て
=0.40という大きな+の横力が発生することになる．
ここでは，ﾄｯﾌﾟﾋﾞｭｰで最大直径である赤道上付近の流れの遷移と剥離位置を 議論したが，実際には遷移と剥離現象は野球ボールの表面上の縫い目位置の影響 を受けて3次元的に変化しており，より複雑な様相を呈していると考えられる．
５．ゆっくりした回転にともなう横力の発生
ゆっくりと回転する野球ボールに回転方向に応じて定常な横力が発生すること は，すでに第1報のFig.9に示した．このような横力が作用している場合に後流 の時間平均速度分布を測定した結果をFig.9に示す．Y軸の+側から見て，時計 方向(CW:●)および反時計方向(CCW:○)に0.5rpsの回転速度で回転させたが， 後流はCWの場合-Z側へ，CCWの場合+Z側へとX軸上からシフトしており，定常横力 がその反力として作用していることと対応している．
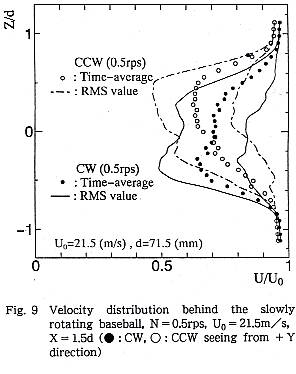
そのメカニズムについては，ボール表面からの流れの剥離に回転方向，特に表面粗 さの進行方向によってヒステリシスが生じていることによるのであろう，と推測でき るが，現在のところ詳細は不明である．ボール境界層の中を縫い目(糸と皮の盛 り上がりによる粗さ)が通過するときに，乱流への遷移と剥離にどのように影 響するのか，という興味ある問題を含んでいる． なお，ボールのゆっくりした回転にともない，縫い目の位置は順次変化するが， 後流の速度欠損がもっとも広いのは，Fig.2で示したようにθ=45゜の場合であ る．Fig.9にはボールの回転にともなう流速の変動成分のRMS値を実線(CW)と1点 鎖線(CCW)で記入する．RMS値の最大値はθ=±35゜のシフトした速度欠損や，θ =45゜の時間平均流速分布の相似形を示す．一方，最小値はFig.2で示したθ= ±35゜のボール配置の場合のシフトした速度欠損になっていると考えられる．
６．Weaverのｺﾒﾝﾄ2)について
Weaverは，前報の参考文献1)のWattsらの論文に，「良いナックルボールは無回転 で投げられる．その後わずかにスピンするから，ボールにスキントルクが作用している． この重要なファクターが見落されている」とコメントしている2)．確かに，第1報の Fig.4に示した観測結果は，投げられたボールが飛翔軌跡のほぼ最高点に達する まで，ほとんど回転しておらず，その後1/4回転している． そこで，硬式野球ボールをできるだけ回転摩擦の少ない回転フリー装置に取付け， 風洞気流の中に第1報のFig.2の配置で挿入し，回転の様子を調べた．その結果， 一方向に回転し，U=20.0m/sで，13rpsの回転速度に達する，ことが分かった． これらの結果は支持装置の摩擦の程度に依存すると考えられるが，硬式野球 ボールは明らかにAuto-rotating機能を持っている．スキントルクが重要なファクターである とする当時カナダのカルガリー大学の4年生であったR. Weaverの指摘は的を得ている．
７．ボール後方の非定常渦の影響
Fig.1，Fig.2でも示したように，非回転のボール後方の非定常渦による流速変動は一様流の２～３％である．ボールに作用するＸ，Ｙ，Ｚ，方向の非定常空気力を０～１００Ｈｚの間で調べたが有意な成分は存在しなかった．非定常空気力の周波数は，ナックルボールの回転速度に比較しても，充分高く，しかもその絶対値は小さい．したがって，硬式野球ボールについてはこの非定常空気力によってボールが変化することはないと考えられる．
８．第2報の結論
野球ボールの縫い目位置変化にともなうWake fieldの再循環領域の時間平均流線を描いた．横力，抗力の特徴的な変化を次のように説明した．
(1)ナックルボールのレイノルズ数は105付近であり，滑面球の遷移レイノルズ数よりも低いけれど縫い目はボール表面の粗さとして作用する．
(2)ボールの配置角度がθ=0ﾟの場合，境界層は層流から乱流に遷移し，前面から±120ﾟで乱流剥離する．その結果，Wake field は小さくなり，小さな抗力係数の原因になる．
(3)θ=+35ﾟの場合，-Z側では縫い目の少し前方の前面 から94ﾟ付近で層流剥離し，+Z側では縫い目の作用 によって境界層は乱流に遷移して剥離位置は110ﾟ付近に後退し，乱流剥離する．その結果，Wake fiel d は-Z 側に大きくシフトし，結果として+Z方向への大きな横力を生ずる．
(4)θ=+45ﾟの場合，±90ﾟ付近に位置する縫い目で流れ は剥離し，Wake fieldの幅は広くなり，+X方向に伸び，抗力が大きくなる．
第１著者が野球ボールの変化球への興味を持つきっかけになる議論を少年時代 から行っている兄と，日頃激励しあっている研究者仲間および球友に感謝します．また財団法人水野スポーツ振興会の平成6年度助成金を受けたことを記し， ミズノ㈱の佐藤文宣，鳴尾丈司，両氏に謝意を表します．この研究を進めるにあたり，卒業研究生は良くがんばってくれました．感謝しています．
１９９４年１０月中旬に行われた北京清華大学での国際会議の宿舎で，第３著者の長男 岡島厚平君（当時，早稲田大学理工学部大学院生）はこの論文の説明を受けて非常に喜んでくれました．しかしながら，２ヶ月後に突然夭折されました．この論文を彼に捧げ，慎んで哀悼の意を表します．
参考文献