pgplotでグラフを書く

数値シミュレーションをおこないながら実時間シュミレーションをしたい場合は， グラフ作成ツールでは無理がある．C++ から呼び出せる，デバイスに依存しない グラフィックスパッケージライブラリが必要になってくる．プログラムを Linux で書くことが多いので，Linux 環境との親和性がよくWindows 2000でも使えるも のが望ましい．Visual Basic はWindows の特徴であるGUI を極めて簡単に作る ことができるが，Mastrix クラスやVector クラスの構築には不向きである．ま た我々にとってLinux 環境で使えないのは問題点の一つである．研究室の卒 業研究では，これまで，ユーザーインターフェイスをVisual Basic で作り，VC++ でアルゴリ ズムを実現したDLL(Dynamic Link Library )をVisual Basic 側からコールする 方法をとってきた．今回はプログラムから直接図を作ることにしよう．そこで， Pgplot Graphics subroutine library を使うことに決めた．Pgplot はもともと Fortran 用のサブルーチン群で，C++ から使うこともできます．Pgplot を用いたプロ グラムをLinux 上で開発し，同じソースファイルをCross Compile 環境でコン パイルすればWindows 2000で走るEXEファイルを作れるので一挙両得である． Pgplot は比較的使いやすく，最初に作成した数値シュミレーションプログラム を修正するだけよい．図2.1と同じグラフを出力するmain() 関数を 示します．cpg で始まる関数がPgplot のサブルーチンである．このプログラムはひとつの画面に一つの図を出力するものであるが，複数の図を入れることも容易にできる．

int main(int argc, char* argv[]){
	
	vector x;		// Eulerian angles x=(alpha, beta ,gamma)
	vector w;		// 回転系角速度
	vector rL;		// 回転系角運動量
	
	double t,h;
	int nsteps, print_interval;
	
	std::ifstream fin(infile, std::ios::in);
	if (!fin.is_open())
	    error(argv[0], infile , ":Cannot open file for reading");

    // 回転軸の天頂角の初期値p(degree), 回転軸の方位角の初期値q(degree), 回転周期の初期値 T(second)
    // 天頂角の初期値のずれu(degree)	 	
	fin  >> nsteps >> print_interval >> T >> p >> q >> u;
	
	// ........ Initialization ..............................
	initial_condition(x,w);      

	h = T/200.0;
	
	cout.precision(16);
        std::ofstream fout(outfile, std::ios::out);
	if(!fout.is_open())
	    error(argv[0], outfile , ":Cannot open file for writing");			
	fout.precision(16);
	fout.setf(std::ios_base::fixed, std::ios_base::floatfield);
	// graphics
	double told=0.0,yold=0.0;
	char *devname="?";
	if (argc == 2)
	    devname =  argv[1];
	if (cpgopen(devname) != 1)	  // open a graphics device
	    exit(1);
	 // change the size of the view surface
	cpgpap(6.0,1);	              
     // set window and viewpoint and draw labeled frame
	double tmin=0.0,tmax=20.0,ymin=0.0,ymax=16000.0;	
	cpgenv(tmin,tmax,ymin,ymax,0,0); 
	cpglab("t(sec)","Lx(angular momentum)"," ");// write labels
	x-axis,y-axis and top of plot	
	
	for(int i=0; i < nsteps; i++){
	    t= h*(i+1)
	    rk4(x,w,dxdt,h);
	    w=omega(x);    // w の再計算
	    rL= A*L;       
	    double E=(I[0]*w[0]*w[0]+I[1]*w[1]*w[1]+I[2]*w[2]*w[2])/2.0; // 回転エネルギー
	    if (((i+1) % print_interval ) == 0){ 
	         //fout << t << "  " << rL[0] << " " << rL[1]<<  " " << rL[2] << " " <<
	         //E << "  " << cos(x[1]) << "\n";
            cpgsci(2);                  // set color index
            cpgmove(told,yold);         // move pen 
             // draw a line from the current position to a point
            cpgdraw(t,rL[0]);         
            told=t;
            yold=rL[0];
	    }
	}
	cpgclos(); close a selected graphics device
	return 0;
}

図 2.5: 角運動量ベクトルの成分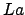$La$の符号は変化しない