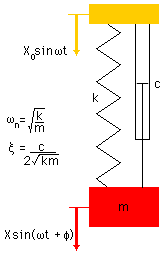
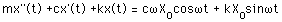
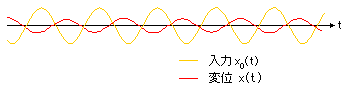
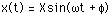
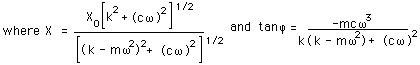
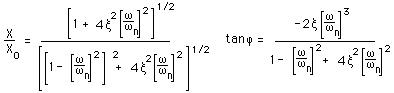
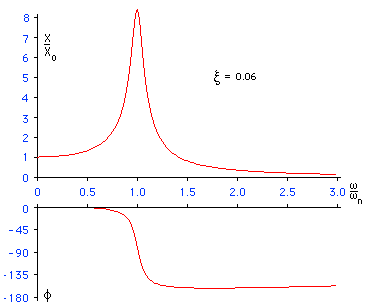
定常状態：固定端入力 支持端が正弦波加振される場合の運動方程式は 典型的な定常状態での振動は以下のように図示できます． 運動方程式の解は，定常状態では 以下のように 求められます． Xは振幅，fは振幅と加振変位との間の 位相角 です． 慣例に従ってこれらの式を 無次元化 しますと，次のようになります これらの式を グラフ化 しますと，以下のようになります グラフ作成時の問題： x に違う値を入れてみて，その効果を確かめて下さい．

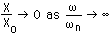
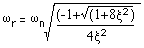
注意： 応答曲線には 共振点 があります． 共振点 での周波数は， There is thus always a resonance. このように，常に共振点を持つことになります． x の値が小さい場合， 応答曲線のピーク は，1/2 x になります． 位相 f は0から-180度の範囲で変化します． ですから応答変位は入力変位に比べて遅れます．でも周波数が高い場合の位相遅れは90度です．