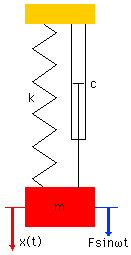
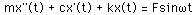
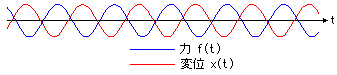
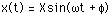
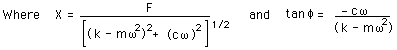
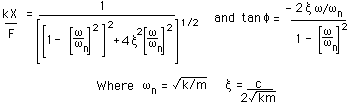
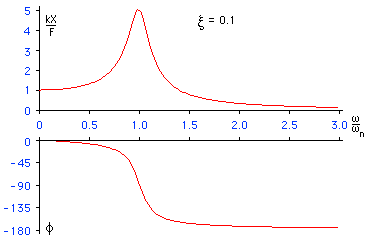
定常振動 - 外力 サインカーブ状の外力を伴う一自由度系の振動は， 典型的な定常振動は以下のようになります． 振動が定常状態に達した場合，ｘ（ｔ）は 以下のように求められます． Xは振幅， f は振幅と力との間の 位相 です． 通常，先に示したような式は 無次元化 して表されますので，これを無次元化しますと次のようになります． これらの式は，次のように グラフ化 できます． グラフィックプログラム： x の値が変わることの影響を確かめてみてください．

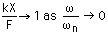
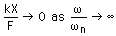
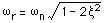
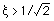
注意： 応答曲線には 共振点 があります． この 共振点 での周波数は，次のようになります． ですから，以下の条件を満たすときには共振点はない（つまり，応答曲線にピークは生じない）ことになります． x の値が小さい場合， 応答曲線のピーク は，1/2 x になります． ですから，小さい x に対しては，この値を 応答曲線のピークから求める ことができます． 位相 f は0から-180度の範囲で変化します． ですから変位（応答）は力（入力）に対して遅ます． ある種の振動解析では，この応答曲線と位相とは リサージュ図形 を求めるために組み合わせて使われます