|
減衰振動
実際の振動システムでは,エネルギが消散します.
言い換えますと,振動は継続せず,必ず減衰します.図に示しましたような質量がない粘性ダンパ(viscous damper)を使いますと,このエネルギが消散するメカニズムを説明できます.
この粘性ダンパには,例えば質量が正方向に運動している場合には負方向の力が生じます.この粘性ダンパに生じる力は質量の速度に依存して変化します.
つまり,粘性ダンパの減衰定数をcとしますと,質量には-cx'(t)という力が付加します.
ですから,減衰が作用する場合の力の釣り合い方程式は,
ニュートンの第二法則
を用いると次のように表すことができます.
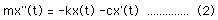
表現を簡単にするために式(2)の両辺をmで割りますと,
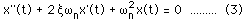
 は先に紹介した
非減衰振動数です.
粘性減衰定数は以下のように定義しています. は先に紹介した
非減衰振動数です.
粘性減衰定数は以下のように定義しています.
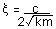
|
![]()