|
定常状態:アンバランス
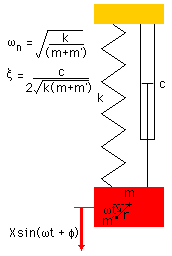
アンバランス質量が定速度で回転している場合の運動方程式は,
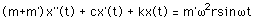
定常状態の解x(t)は次のように
表すことができます
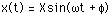
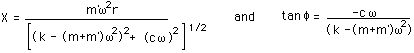
Xは振幅,
fは変位とアンバランス力との間の
位相角
です.
慣例にしたがって,分子分母をkで除して無次元化しますと,
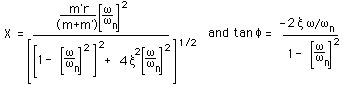
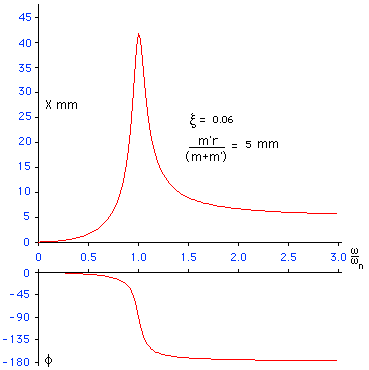
これらの式は,以下のように
グラフ化
できようかと思います.
グラフを作るときに:
x
に違う値を入れてみて,その効果を確かめてください.
  
|
注意:
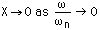
回転しませんと加振力が生じませんから,定常振動も起こりえません.
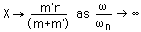
これは質量mとm'の中心が動かない条件です.
応答曲線には
共振点
があります.
共振点
の周波数は以下のようになります.
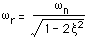
(この値は非減衰固有振動数よりも大きくなっています!)
以下の条件では共振点はない,つまり応答曲線にピークは表れません.
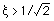
位相
は0から-180度の範囲で変化します.ですから変位(応答)は力(入力)よりも遅れます.
|
![]()