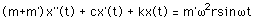
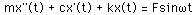
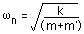
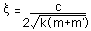
定常速度 アンバランス質量が一定の速度( a = 0) で回転している場合，運動方程式は次のようになります． この方程式は， 正弦波外力 が作用する場合の運動方程式と極めてよく似ています．, システムの全質量はm+m'です． ですから， 非減衰固有振動数 は次のように求められます． また， 減衰比 は以下のようになります． 減衰比 や 非減衰固有振動数 が異なると，定常状態に達するまでにどの程度振動しなければならないのか，という点に関しては， アニメーションプログラム を走らせて，実際に確かめてみてください．.	アニメーションプログラム
運動方程式に対する数学的な解は，色々な方法で求められます． 初期の過渡的な振動の後（過渡振動は初期状態や，アンバランス質量が一定の角速度で回転を開始し始めるときの起動効果に依存して変化します）， 振動は正弦波状の定常振動に達します．この定常振動状態のことを， 定常状態 と呼びます．	注意： アニメーションプログラムを走らせる時， 場合によっては過度に振動するような加振条件を選ぶと思います．この場合，粘性ダンパがその駆動範囲を超えますので，加振条件は制限されます．